When Applicants Warp Your Bell Curve
Job applications pour in; you sift and sort, and are happy when there are plenty of qualified applicants, worried when there aren’t enough. The numbers are that simple to understand and sort—or so you think.
You think the detailed statistics don’t matter—specifically, you don’t care how that talent is distributed among the applicants, e.g., whether or not the truly well-qualified in your applicant pool are, as a percentage of the total, over or under-represented in the group you are vetting, relative to the general population or to the norm in your industry or company.
Similarly, you assume that your testing protocols have no bias that may conceal or exaggerate applicant talents, or skew or shift the talent curve, e.g., a personnel test that is too easy or too hard.
All that matters, you think, is the absolute numbers of high scorers, whether there are enough of them to ensure a good pick and that you know how to pick them.
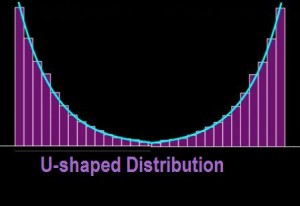
You could care less whether the talent pool is, like IQ, distributed in a symmetrical bell curve (with a single hump and proportionally fewer outstanding and fewer truly dismal applicants), in a “bimodal” curve with two camel peaks, in a curve with an off-center peak at the far right or the far left, or distributed in a curve shaped like a “U”.
Alas, things are not so simple. In particular, as will be show below, how that talent is actually distributed and why it is has implications for how well and wisely applicants are being evaluated, including in the process of formal testing.
When Curves Can Throw You a Curve
Even as long ago as 1948, researchers urged caution in interpreting the significance of employment test results, including their distribution:
“..The distribution of employment test scores is shifted toward the higher end of the scale. It was speculated that it could be due to the word getting around among applicants, resulting in only better applicants applying for the job. It is viewed that the shift could be due to test-taking incentivation. The authors made follow-up analyses of employees in industrial plants. It is concluded that the mere presence of tests in the employment office cannot guarantee highly qualified applicants, and that the tests must be validated for the positions applied.” (“Additional Distributions of Test Scores of Industrial Employees and Applicants”, MacMillan, Myles H.; Rothe, Harold F., Journal of Applied Psychology, June 1948, Vol. 32 Issue 3)
If you are forced to consider such statistical data, you may expect the credentials of job applicants to fall into a bell curve, i.e., to be “normally distributed”.That means that you may, on the basis of your experience or understanding of odds, expect them to be (close to) average, with those with extremely good or extremely bad credentials, including test scores, being, by comparison, rare, as a percentage of the total.
In this respect, and if your hunch is correct, resume gathering should resemble IQ testing—the results should, when displayed as a graph, resemble the familiar bell curve. The greater the number of variables determining the final score, the likelier it is that the curve will be a bell (while allowing that the “spread”, i.e., variance or “standard deviation” may be narrower or the mean shifted, probably to the right).
Since numerous variables, e.g., education, nutrition, motivation and genes, determine both job credentials and IQ test scores (as is the case with variables such as body weight measures or reindeer antler size), it is, according to the underlying statistical theory, to be expected that data representing them should, when plotted, have a bell shape.
But, suppose they don’t; suppose, for example, that instead of 5% of your applicants being outstanding on your informal 1-10 scale, 90% are, and that no matter how much you attempt to reasonably tighten your standards, 90% of the applicants still look very, very good.
In that instance, the Taco Bell or Liberty Bell curve you expected is replaced by a curve with the bulge shifted to the far right, at the expense of the far left, which is now dramatically flattened. How would you interpret this and does it matter?
Even if you are among the many who glaze over like a bell-shaped vase baking in a kiln when graphs and formulas are mentioned, you can still think about the implications of a “skewed” (asymmetrical, with the hump bumped to the right or left) graph of an applicant database of scores or ratings.
Why the Weird Skewing?
Some of the commonsensical explanations of such an unusual skewing include the following:
To keep things simple, imagine you are looking at a bar chart of applicant test scores, which resembles the chart shown here: the higher the score, the greater the number or percentage of applicants with that score.
The right-skewed result you observe in your sample may be evidence of lax selection criteria —for example, either because of a design failure or because of an unacknowledged or unrecognized spike in ability in the general population, much like the result one would get if administering an IQ test from 70 years ago to a crop of new and young recruits (because of the “Flynn Effect”, viz., the shift in mean IQ from 100 to about 115 as the new “average”).
However, if the unusually high scores are a recent effect and a dramatic departure from previous long-term averages, the lax criteria explanation can be ruled out.
If the test or the criteria are relatively new, both explanations for the high scores remain available: Either the HR criteria are not stringent enough or the general population’s capabilities and performance have improved.
That said, there remains another possible explanation of the unusually numerous high scores: a severe job supply-demand imbalance, with too many applicants chasing too few jobs. In that instance, it would not be surprising that not only would competition for the few available jobs be intense, and that there would be an over-supply of highly-qualified applicants, but also that also many of the less qualified, daunted by the horrible odds, would just give up and not bother to apply, as suggested in the research quote above.
In that scenario, the statistical over-abundance of high-end performers reflects a severe employment supply-demand imbalance, with job seekers vastly outnumbering job openings.
On the other hand, suppose that your in-house recruit data do resemble a Taco Bell, but that the average score is much higher than what the HR department was used to seeing and expected. That is to say, the normal bell curve has shifted to the right, with a higher average.
For example, suppose the average score, which used to be 70 out of 100, has recently and consistently been 90, with virtually all scores falling between 85 and 95. Unlike the skewed bar graph described above, this one is quite symmetrical.
How is this to be interpreted, when just like the skewed results, these fall almost entirely in the far-right high-score zone?
One possibility is that your test never changes and that the questions (and answer analyses) have circulated in the applicant pool, which, if the case, warrants an overhaul of your test or test security.
Another possibility is that as “the word” gets around regarding your use of a given test, “incentivized” applicants undertake intense preparation for it, where possible.
Alternatively, the data may suggest a wholesale shift to higher levels of performance and capability in the general population, which the HR test is sampling, e.g., as a result of something like the Flynn Effect.
In that case, HR may have an opportunity to raise employment standards and get more bang from the employee buck. The older the test used, the likelier this possibility.
Of course, neither you nor the hiring company is likely to care what the explanation is, so long as there are enough well-qualified applicants to choose from, relative to the job demands and expectations.
However, this can be a short-sighted, narrow perspective, especially if the test results and applicant pool are being misunderstood.
For example, that abundance of excellent applicants might be attributable to a failure of the employer to keep up with rising industry employee performance standards and outcomes, and to therefore lag behind the pack.
Despite this age of virtually instantaneous communication and rapid dissemination of standards, such a standards gap cannot be entirely ruled out.
Likelier than this is the possibility that even though the HR department is well aware of such rising standards, it may not have devised the best measures of these in its in-house evaluations.
Navigating a U-Curve
Suppose you get, instead of any kind of a bell curve, a “U-curve”, i.e., a distribution with lots of applicant scores or credentials only at the extremes, namely, the very good and the very bad, with few middling performers.
If there are enough outstanding applicants in that curve’s far-right group, you probably won’t be concerned about why the curve is U-shaped. But perhaps you should be.
One reason is that a U-shaped talent, skill, test, etc., curve may distort the data you are really interested in if some extraneous variable is allowed to exert a strong and misleading influence.
For example, if your goal is to test IT engineers design skills using a standardized test of some sort, the resulting scores may display as a U-curve rather than a bell curve. How could that happen? I
t could be caused by testing the engineers in a language that for many of them is an imperfectly mastered second language, e.g., English, when they are from China, the Middle East, etc.
Those who are both excellent IT engineers and very competent English speakers are likely to achieve high scores, if the test is very language dependent (as opposed to pattern-recognition tests, which are much less so).
Those who are only excellent IT engineers with poor English-language skills may achieve very low scores. If superb English skills are required to do well on the test, there may be very few middle-range scores, and, of course those who are weak in both the IT and language domains will perform the worst.
When there is a strong positive correlation between language skill and professional skill, a very pronounced U-curve is even likelier. This was a phenomenon I observed in teaching subjects such as calculus to Chinese students: The students who had the best grasp of English also had the greatest mastery of the math—a kind of “double-blessing” for them; those worst in one were also worst in the other.
Bias Warp
An example of a commonly used applicant test that may be vulnerable to such a U-curve result is the Miller Analogies Test, primarily used in graduate school admissions, which requires the test taker to complete analogies such as “retributive justice is to forbearance as restorative justice is to ?” or “Mozart is to classical music as Wagner is to ?”, with the correct answer appearing among multiple choices.
It stands to reason that anyone with the verbal facility and broad cultural knowledge to nuance such language is very likely to have comparably strong analogical reasoning skills, since detecting verbal and conceptual similarities through analogies is the flipside of being able to detect subtle differences between concepts.
If my experience with Asian test-takers is a reliable guide, I would expect a group of job applicants comprising a significant number of non-native English speakers to be very likely to have scores distributed in a U-curve pattern on the M.A.T. and other language/culture-dependent tests.
Given the possible impact of extraneous variables such as native language and culture, it is important not to mistake a low score on such a biased test as a reliable measure of the skills presumably being tested for.
However, to the extent that sophisticated language skills are as essential as technical and other professional skills, such test biases may in fact function as useful filters.
To sum up, when evaluating job applicants by their test scores, be alert for
- U-shaped, shifted or skewed distributions that may reflect
- the strong influence of an extraneous, uncontrolled variable (such as language or culture)
- the possibility that higher than expected average scores may reflect a shift in the industry or population standard (results)
- a “leak” of test content secrets into the applicant pool
- a relaxing of your in-house test-content standards
- recently introduced flaws in test design (e.g., validity and reliability)
- intense prepping in the applicant pool
- demoralization of all but the most qualified (resulting in only the latter applying for the job and being tested)
- Other labor supply-and-demand influences on test score range and distribution(like those discussed above).
Distilled to their absolute essence, these cautionary observations suggest you should be especially alert for any sudden anomalies in test-score or other evaluation distributions that set off alarms…
…especially alarm-bell curves.